Making explainability algorithms more robust with GANs

31 Jul 2020

Japanese below | Comments

Explainability algorithms like LIME (Locally Interpretable Model-agnostic Explanations) (Ribeiro et al., 2016) have gained much popularity in both academia and the industry. For the latter, making complex machine learning models interpretable means bridging the trust gap that often manifests between machine learning systems and their end users, which can become an important factor for successful adoption.

My previous blog posts focused on the robustness of machine learning models against adversarial attacks, showing that neural networks are susceptible to the slightest of perturbations of the input.

It turns out that even explainability algorithms are not immune to similar threats. In this blog post, we will look into the vulnerabilities of LIME as well as an attack which exploits this. We will then talk about a proposed defense from a recent paper which I worked on called Improving LIME Robustness with Smarter Locality Sampling, to be presented at the 2nd Workshop on Adversarial Learning Methods for Machine Learning and Data Mining @ KDD 2020. Code for this work can be found here.

Attacking LIME

In a previous blog post, we discussed the basic formulation of additive feature attribution models, a class of explainability algorithms to which LIME belongs. Mathematically, it tries to minimize the following loss function:

\[\begin{align*} \pi_{x}(z) &= exp(\frac{-D(x, z)^2}{\sigma^2}) \\ L(f, g, \pi_x) &= \pi_{x}(z) \left ( f(z) - g(z') \right )^2 \end{align*}\]

where the explainer $g$ tries to mimic the target black-box model $f$’s behavior for a set of synthetic samples $z$, and the loss is weighted by $\pi$ which represents the distance between synthetic samples $z$ and the original data $x$ (hence “locally interpretable”). You will also recall that LIME needs to generate these synthetic samples $z$ in order to query $f$ - this acts as a way to understand the behavior of $f$ without peeking into the implementation or parameters of $f$, thereby making LIME a model-agnostic method.

In particular, LIME generates samples by perturbing data with noise sampled from a unit Gaussian $\mathcal{N}(0,\,1)$. Unfortunately, it is this sampling procedure which makes LIME susceptible to exploitation. Slack et al. have recently discovered that this naive sampling strategy leads to synthetic data $z$ which are out-of-distribution (OOD) .

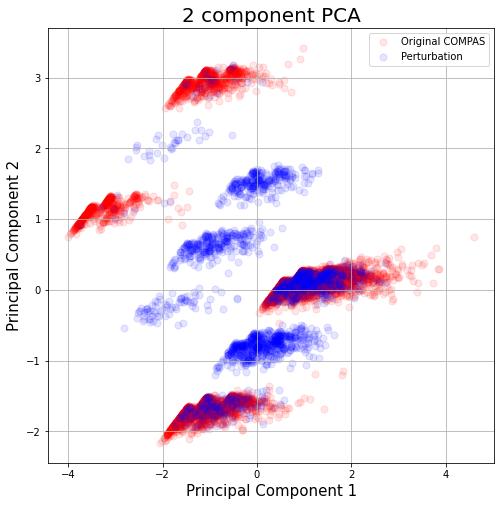
As Figure 1 shows, there is a significant discrepancy between LIME samples and original data from the COMPAS dataset. In fact, LIME samples are identifiably OOD, and Slack et al. exploit this flaw to construct their attack, which we refer to as the Fooling LIME attack.

Imagine an adversary that wants to deploy some biased, harmful machine learning model to production. A biased model could be one that makes its decisions solely on sensitive features like sex and race. For example, the algorithm below decides whether a given convict would commit another offense once out prison and relies solely on race:

\[\begin{equation} a(x)= \begin{cases} 1,& \text{if } x_{race} = \textit{"African American"}\\ 0, & \text{otherwise} \end{cases} \end{equation}\]

Now suppose that the model must go through some auditory process to detect any harmful behavior. Assuming that the implementation of the model/solution is hidden from the auditor for the sake of intellectual property, the auditor may naturally elect to use model-agnostic explainability algorithms like LIME to understand the target model’s behavior further.

This is where the attack is executed. Knowing that LIME’s synthetic samples are identifiably OOD, the adversary can train a binary classifier $c$ that predicts whether a given input is real or not. The attacker then can use $c$ as part of a scaffolding function; as formulated below, a data sample is routed to the original, biased model only if the $c$ decides that the sample is real. If it detects a LIME sample, it instead routes the sample to an innocuous model $\psi$ that doesn’t rely on sensitive features.

\[\begin{equation} s(x)= \begin{cases} a(x),& \text{if } c(x) \geq 0.5\\ \psi(x), & \text{otherwise} \end{cases} \end{equation}\]

In other words, LIME would only see predictions from the innocuous model and would hence determine that the adversarial model is not biased.

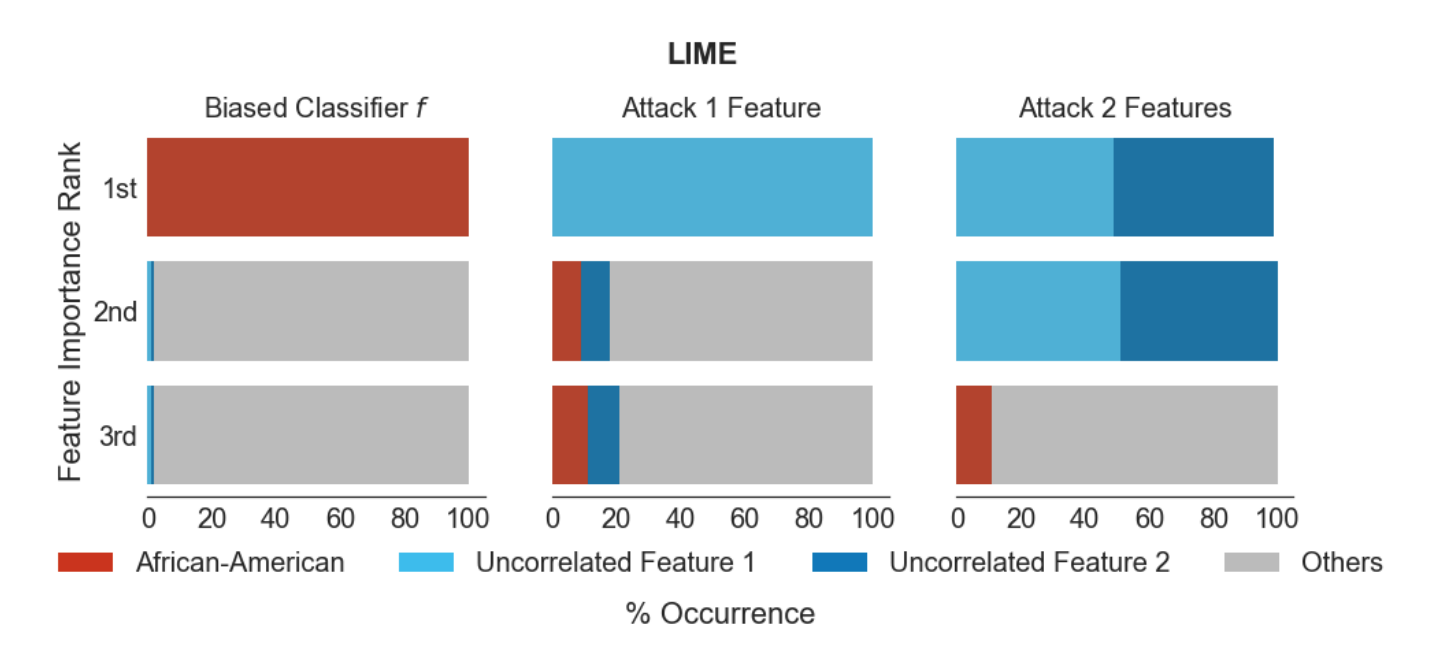
The results reported in Fooling LIME and SHAP: Adversarial Attacks on Post hoc Explanation Methods show that the Fooling LIME attack can circumvent LIME effectively across several real-world datasets (Figure 2).

Defending LIME with GANs

Can we defend against the Fooling LIME attack and make LIME more reliable? Note that the attack relies on having a critic model that can accurately distinguish between real and fake samples. What if we can generate synthetic samples that are realistic? This leads to our proposal: make LIME more robust by replacing its naive sampling strategy with generative adversarial networks (GAN).

In particular, since we are focusing on tabular datasets, we use the Conditional Tabular GAN as our sampler as it provides a better modelling of discrete and continuous features (Xu et al., 2019). Through adversarial learning with the discriminator, CTGAN learns to generate data that is more realistic compared to what comes out of LIME’s sampling method.

CTGAN is conditional in that it receives two inputs - a random noise vector common to vanilla GANs and a conditional vector that selects a particular category among the categorical features. CTGAN is “conditioned” to generate data according to the selected category which allows for more diversity in the outputs. While in the original CTGAN this conditional vector is sampled randomly, we condition CTGAN based on the actual categorical features of the given input instead:

\[\begin{equation} \begin{aligned} & \tilde{X} = && g(z, m_x) \\ & m_{d_i}^{k} = && \begin{cases} 1,& \text{if } k = x_{d_i}\\ 0, & \text{otherwise} \end{cases} \text{for } k = 1, \dots, |D_i| \\ & m_x = && m_{d_1} \oplus m_{d_2} \cdots \oplus m_{d_n} \\ \end{aligned} \end{equation}\]

where $\tilde{X}$ are the synthetic samples generated by $g$, the CTGAN generator. This helps CTGAN generate synthetic samples that are more local with respect to the given data sample to be explained. We also use the CTGAN discriminator to filter out any unrealistic samples generated by $g$:

\[\begin{equation} \tilde{X}_{filtered} = \{x | x \in \tilde{X}, d(x) \geq \tau\} \end{equation}\]

where $\tau is a scalar threshold. We refer to our method as CTGAN-LIME.

Experiments and Results

Our proposed defense is straightforward, but can it make LIME more robust? Here, we present our experiments and results. We first run through our experimental settings.

Black-box and white-box

We experiment with two adversarial settings, namely black-box and white-box. In the former, the adversary does not have access to the explainer nor its implementation; it only receives queries from it. In our experiments, we attack CTGAN-LIME using the original Fooling-LIME attack, which trains its critic $c$ based on synthetic samples generated by the LIME strategy. This establishes a baseline measure of robustness for CTGAN-LIME.

However, to further fortify our investigation, we also conduct experiments under the white-box setting, where we assume that the adversary now has increased access to explainer, including its specifications, implementations, and even its parameters. In our white-box experiments, the attacker has full access to the CTGAN generator of CTGAN-LIME. In other words, the attacker generates training data for $c$ from the same sampler which the explainability model uses to generate explanations. This is a strictly stronger adversarial setting than the black-box counterpart and provides a stronger evaluation of robustness.

Evaluation

We measure the robustness of an explainability algorithm based on top-k accuracy, or the proportion of explanations which correctly identify the sensitive feature (e.g. race, gender) to be among the top $k$ contributing features for the adversarial model. In other words, this represents how well the explainability model is able to detect biased behavior.

Datasets

Finally, here are the datasets we experimented with:

• COMPAS recidivism (Larson et al., 2016): A dataset where the task is to predict whether a given criminal defendant will commit another offense. The sensitive feature used by the biased classifier $a$ is race.
• German credit (Asuncion & Newman, 2007): A dataset which classifies how good or bad a given loan applicant is. The sensitive feature is gender, and the biased classifier predicts “good” if Gender = “male” and “bad” if otherwise.
• Communities and crime (Redmond & Baveja, 2002): A dataset which measures various socio-economic and law-enforcement variables of communities in the US. As done in (Slack et al., 2019), we convert the dataset into a classification task whereby a community is labelled “high-crime” if the violent crime rate is above the median and “low-crime” otherwise. We designate the white population proportion as the sensitive attribute. The biased classifier predicts “high-crime” if $\textit{white population proportion} < 0.5$ and “low-crime” if otherwise.

Results

We now look at the top-k accuracies across each attack and dataset. Table 1 shows the top-k accuracies for each black-box attack.

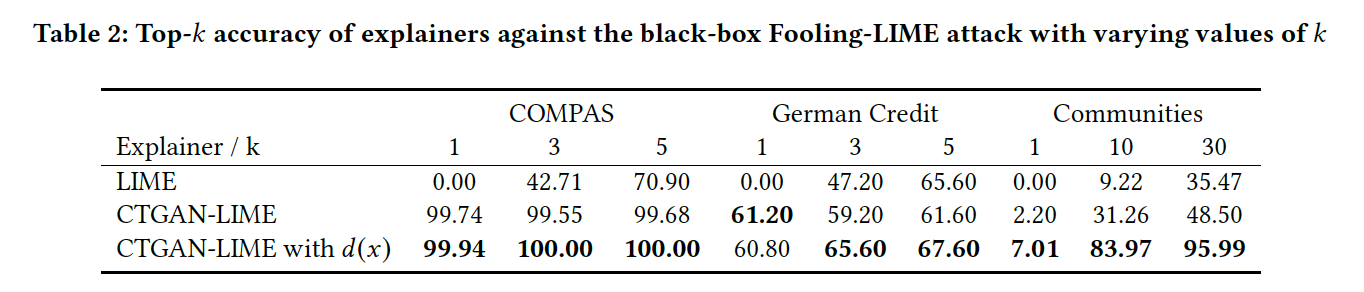
As we can see, CTGAN-LIME achieves higher accuracy than LIME for each dataset, indicating that it can better detect biased behavior of the adversarial model across different datasets.

Table 2 displays results for each white-box attack.

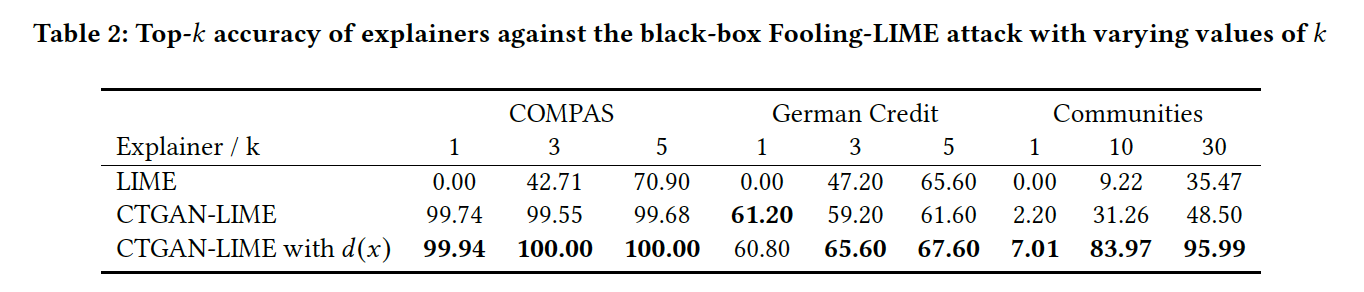
In the white-box attack setting, the attacker has access to the CTGAN model and its parameters, thereby enabling the attacker to execute a more effective attack. Indeed, Table 2 displays a decrease in accuracy of the CTGAN-LIME model. However, we also note that the accuracy CTGAN-LIME is still higher than that of LIME, indicating increased robustness overall; in fact, the Fooling-LIME attack using the CTGAN sampler is slightly more effective than the original attack. Finally, we observe that the discriminator $d(x)$ which filters low-quality samples helps improve the accuracy of CTGAN-LIME further.

Explanation quality

Finally, making LIME more robust wouldn’t make sense if the resulting explanations were not up to par in terms of quality. Hence we also compared explanation quality between CTGAN-LIME and LIME via the precision metric used in (Ribeiro et al., n.d.):

\[\begin{equation} precision(E) = \mathop{\mathbb{E}}_{Q(x'|E)} \left [ 1_{f(x)=f(x')} \right ] \end{equation}\]

Intuitively, this metric measures the agreement between the model’s prediction $f(x)$ and the model’s prediction on other samples which are similar to $x$ according to the features identified as influential in $E$. The higher this number, the more the explanation is aligned with the model’s behavior.

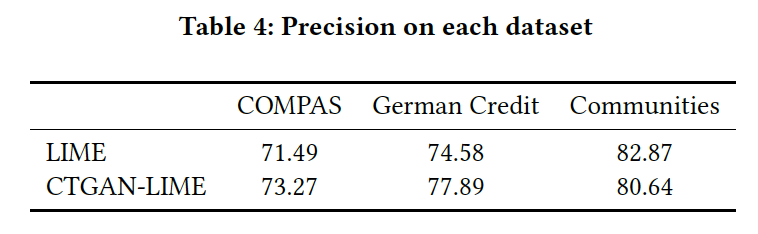
As the table above shows, the precision of CTGAN-LIME is comparable with that of LIME across each dataset.

With that, we show empirically that CTGAN-LIME exhibits higher robustness while maintaining comparable explanation quality as LIME.

Summary

In this blog post, we have looked at how LIME can easily be fooled to miss biased behavior from harmful models by exploiting its naive sampling strategy. We introduced CTGAN-LIME, a method inspired by generative adversarial networks to make LIME more robust against such attacks. To our knowledge, this is the first attempt to make explainability algorithms more robust; we hope future work continue to make algorithms like LIME more robust and reliable. Do check out our paper for more details, and feel free to reach out if you have any questions. Thanks for reading!

GANを用いて判断解釈モデルLIMEを敵対的攻撃から守ってみた

Back to English

アカデミアやインダストリーではLIME (Locally Interpretable Model-agnostic Explanations) などと言った機械学習の判断解釈モデルへの注目度が高まっており、特に後者においてはneural networkなどを用いたソリューションをよりエンドユーザーにとって解釈・扱いし易くするためにLIMEが用いられていたりします。

しかし、LIMEのようなアルゴリズムにも最近脆弱性が見つかっており、それを利用したadversarial attack (敵対的攻撃)が発表されています。今回の記事では、その脆弱性に着目した上で私が開発に関わったLIMEの頑健性（robustness）を上げる防御的手法（Improving LIME Robustness with Smarter Locality Sampling）について解説して行きたいと思います。尚、この手法はKDD 2020の2nd Workshop on Adversarial Learning Methods for Machine Learning and Data Miningに採択されており、手法に関する実装・コードはこちらにてご参照頂けます。

LIMEの脆弱性とそれを利用した攻撃

先ずはLIMEについて少しおさらいです。前の記事にも書いてありましたが、LIMEは線形モデル$g$を説明対象となるモデル$f$の局所的な挙動に近似させるように最適化することによって各特徴量の重要度を算出します。

\[\begin{align*} \pi_{x}(z) &= exp(\frac{-D(x, z)^2}{\sigma^2}) \\ L(f, g, \pi_x) &= \pi_{x}(z) \left ( f(z) - g(z') \right )^2 \end{align*}\]

上の数式において$z$はサンプリングした擬似データであり、これで対象モデル$f$をクエリし、$(z, f(z))$のペアをいくつか用意することによって局所的な挙動を表すデータセットを構築することができます。このサンプリング手法は、具体的には元のデータ$x$に正規分布$\mathcal{N}(0,\,1)$からサンプリングしたノイズを加えて$z$を生成するという割と簡易的な物です。そしてこのサンプリング手法こそがLIMEの脆弱性の要因であることが最近の研究結果で分かりました。Slack et al.によると、LIMEのサンプリング手法によって得られた$z$のほとんどがout-of-distribution (OOD)・分布外であるとのことです　(Slack et al., 2019)。

上記の２次元主成分分析のグラフを見て分かる通り、確かに元のデータとLIMEのサンプルの分布が不一致です。即ちLIMEのサンプルは特定しやすいことが分かります。これがLIMEの脆弱性です。

Slack et al.はこの脆弱性を利用した敵対的攻撃手法（Fooling-LIME attack）を発表しています。まず、攻撃の設定としては、ある攻撃者が害的なバイアスを持った機械学習モデル$a$（e.g. 人種・性別だけに頼って人種差別・性差別的な判断を出すモデル）のデプロイ・活用を目指していて、デプロイ前に行われる害的挙動の検知を目的とした監査プロセスを回避することを前提としています。尚、監査役の第三者は知的財産保護等の理由により攻撃者のモデルの実装を見ることができないため、LIMEなどの判断解釈モデルを用いることを前提としています。バイアスの持ったモデルは例えば以下のように実装されたりしています。

\[\begin{equation} a(x)= \begin{cases} 1,& \text{if } x_{race} = \textit{"African American"}\\ 0, & \text{otherwise} \end{cases} \end{equation}\]

被告人が黒人だったら再犯率は100％だろうという、人種差別を体現したモデルです。では攻撃者はどうやってLIMEを回避するのでしょうか。前述にある通り、LIMEのサンプル$z$は特定ができるため、攻撃者は本物のデータとLIMEのサンプルを合わせたデータセットを構築し、それらを区別する分別機$c$を学習します。これを基に、攻撃者は以下の仕分け関数$s$（scaffolding function）を実装します。

\[\begin{equation} s(x)= \begin{cases} a(x),& \text{if } c(x) \geq 0.5\\ \psi(x), & \text{otherwise} \end{cases} \end{equation}\]

あるインプットを$c$が本物（LIMEによるものではない）だと判断した時のみバイアスを持ったモデル$a$を適用し、LIMEからきたインプットは、バイアスを表さない別のモデル$\psi$に導かれるという仕組みです。$\psi$からの挙動しか見れないLIMEは当然バイアスを検知することができません。従ってこの手法を用いて攻撃者はLIMEを回避することができるのです。

この攻撃手法を提案した論文（Fooling LIME and SHAP: Adversarial Attacks on Post hoc Explanation Methods）によると、確かにこの攻撃を用いることによってLIMEによる害的バイアスの検知率がかなり低くなることが以下の表で分かります。

GANを用いた防御

LIMEへの攻撃手法・Fooling LIMEを紹介しましたが、どうすれば防御できるのでしょうか。問題の根幹はLIMEのサンプルがあまりにも本物とかけ離れているだと言えます。これにより攻撃者はLIMEサンプルと本物のデータの区別をつけることができる分別機$c$を学習することができるからです。もし$c$が特定できないほどリアリティのあるデータを生成することができれば、攻撃を防ぐことが可能かもしれません。そこで我々は、ただノイズをデータに加えるより、よりリアリティのあるデータの生成を学習するgenerative adversarial networks (GAN) を用いればLIMEの頑健性は上がるのでは、と我々は仮説を立て、LIMEの正規分布によるサンプル手法に代わってGANを用いることを提案しました。

また、今回はテーブルデータだけを扱っているので、テーブルデータの生成に特化した Conditional Tabular GAN (CTGAN) (Xu et al., 2019)を用いることにしました。名の通り、CTGANは条件付きGANの一種であり、インプットは従来の潜在変数に加えてgeneratorの生成データに影響を与えるカテゴリーベクトルの二つから成ります。Generatorとdiscriminatorは敵対的学習手法によってよりリアリティのあるデータの生成を目指して学習します。

また、元のCTGANではランダムにサンプルされるカテゴリーベクトルではなく、説明対象であるデータ$x$のカテゴリー情報をインプットとして用いることによってより$x$に近いデータの生成を促します。

\[\begin{equation} \begin{aligned} & \tilde{X} = && g(z, m_x) \\ & m_{d_i}^{k} = && \begin{cases} 1,& \text{if } k = x_{d_i}\\ 0, & \text{otherwise} \end{cases} \text{for } k = 1, \dots, |D_i| \\ & m_x = && m_{d_1} \oplus m_{d_2} \cdots \oplus m_{d_n} \\ \end{aligned} \end{equation}\]

ここで$\tilde{X}$はCTGANのジェネレータ$g$によって生成されるデータを指します。また、CTGANの学習から得られるdiscriminator $d$を用いて、$g$の生成データのうち、リアリティが低いとみなされたデータをフィルタリングできます。

\[\begin{equation} \tilde{X}_{filtered} = \{x | x \in \tilde{X}, d(x) \geq \tau\} \end{equation}\]

ここで$\tau$はリアリティの閾値を指します。以後、この手法を CTGAN-LIME と称します。

実験及び結果

CTGAN-LIMEは、LIMEのサンプル手法をGANに変えるだけで頑健性が上がるというシンプルな手法ですが、果たしてFooling LIME攻撃を防ぐことはできるのでしょうか。最初に実験の設定を解説します。

Black-box and white-box

先ずは攻撃設定を説明します。Adversarial machine learningは基本的には black-box　と white-box　という二つの攻撃設定があります。前者は、攻撃者が攻撃対象モデルへのアクセスが無い、あるいは制限されているという仮定です。実験では、攻撃者はCTGAN-LIMEの内側について何も知らないという設定で、分別機$c$もオリジナルLIMEのサンプル手法から得られたサンプルデータを基に学習されています。今回の研究ではこれをオリジナルLIMEとの頑健性を比べるベースラインと設定しています。

逆に、white-box 設定では、攻撃者は対象モデルへのアクセスがより拡大していることを想定しています。例えば、対象モデルの設計、実装、そしてパラメータまでもを利用して攻撃することができる設定です。実験では、攻撃者はCTGAN-LIMEがサンプルの生成に用いるCTGAN generator $g$にアクセス権を持っており、同じジェネレータを使って分別機$c$の学習データを生成することができます。言うまでもなく、この設定の方がblack-boxより強力な攻撃を実行できることができ、CTGAN-LIMEの頑健性をより深く検証することが期待できます。

検証に用いる指標

実験では頑健性の測定に top-k accuracy という指標を用います。これは、$n$個の説明のうち、バイアスの要因になるセンシティブな特徴量（人種、性別など）が重要度で上位$k$に入る割合がどれくらいかを測っています。言い換えれば、LIMEがどれだけ攻撃を防ぎ、害的バイアスを検知できるかを測定しています。

データセット

実験に用いるデータセットは以下の通りです。

• COMPAS recidivism (Larson et al., 2016): 有罪の判決が出た被告人による再犯の有無を記録したデータセット。前述のように、攻撃者のモデルは　人種　のみを見て判断する。
• German credit (Asuncion & Newman, 2007): ローン申告者の可否を記録したもの。攻撃者モデルは 性別 を見て判断する。
• Communities and crime (Redmond & Baveja, 2002): 地域別の凶悪犯罪率など、様々な社会・経済指数を纏めたもの。攻撃者モデルは地域の 白人率 を見て、白人率が過半数を超えた場合は犯罪率が低い、下回った場合は犯罪率が高いと判断する。

結果

さて、以下に実験の結果を纏めました。Table 1は、black-box 攻撃　に対するLIME及びCTGAN-LIMEのtop-k accuracyを表しています。

見ての通り、全てのデータセットにおいてCTGAN-LIMEの方がより高い精度を出していることが分かります。また、以下のTable 2では white-box 攻撃 に対する各モデルのtop-k accuracyを記載しています。

前述の通り、white-boxの方が攻撃者がより有利な立場から攻撃を実施することができます。従って、Table 1と比べて、CTGAN-LIMEの精度が低くなっていることが見られます。しかし、それでもLIMEの精度より高いことから、LIMEよりCTGAN-LIMEの方が頑健性が高いことが言えます。また、CTGANのdiscriminator $d(x)$でフィルタリングを施したモデルでは、top-k accuracyが更に高くなっていることが分かり、フィルタリングが効果的であることを示しています。

説明の精度

最後に、CTGAN-LIMEによる判断解釈がLIMEのものと同等のクオリティであるかを検証しなければなりません（もしクオリティが劣っていたら元も子もないので）。そこで、(Ribeiro et al., n.d.)で使われている precision という指標を用いて判断解釈のクオリティを比べます。

\[\begin{equation} precision(E) = \mathop{\mathbb{E}}_{Q(x'|E)} \left [ 1_{f(x)=f(x')} \right ] \end{equation}\]

このprecisionという指標は、説明対象モデルの判断$f(x)$が、判断解釈$E$で重要だと判断された特徴量を基に得られる$x$の近似データにおける対象モデルの判断がどれくらい一致しているかを測定しています。この指標が高ければ高いほど、判断解釈モデルが説明対象モデルの挙動により近似していると言えます。

上記の表にあるように、各データセットにおいてCTGAN-LIMEとLIMEの判断解釈のクオリティに大きな差異があるとは言えません。従って判断解釈のクオリティもオリジナルLIMEそのままです。

以上により、CTGAN-LIMEが同等な判断解釈のクオリティを保ちながらより高い頑健性を備えていることが実験で確認できました。

まとめ

最後になりますが、今回の記事では以下のテーマを取り上げました。

• 判断解釈モデル・LIMEの脆弱性とそれを利用した攻撃手法
• CTGANを使ったLIMEの頑健性の強化と検証

以上となります。これをきっかけに、より高い頑健性を持った機械学習モデル・判断解釈モデルが開発され、産業にも通用するようになれば幸いです。

ご質問・訂正等がありましたら是非ご連絡下さい。最後まで読んで頂き有難うございました！

References

1. Ribeiro, M. T., Singh, S., & Guestrin, C. (2016). "Why Should I Trust You?": Explaining the Predictions of Any Classifier. http://arxiv.org/abs/1602.04938
2. Xu, L., Skoularidou, M., Cuesta-Infante, A., & Veeramachaneni, K. (2019). Modeling Tabular data using Conditional GAN. http://arxiv.org/abs/1907.00503
3. Larson, J., Mattu, S., Kirchner, L., & Angwin, J. (2016). How we analyzed the COMPAS recidivism algorithm. ProPublica (5 2016), 9.
4. Asuncion, A., & Newman, D. (2007). UCI machine learning repository.
5. Redmond, M., & Baveja, A. (2002). A data-driven software tool for enabling cooperative information sharing among police departments. European Journal of Operational Research, 141(3), 660–678.
6. Slack, D., Hilgard, S., Jia, E., Singh, S., & Lakkaraju, H. (2019). Fooling LIME and SHAP: Adversarial Attacks on Post hoc Explanation Methods. AIES 2020 - Proceedings of the AAAI/ACM Conference on AI, Ethics, and Society, 180–186. http://arxiv.org/abs/1911.02508
7. Ribeiro, M. T., Singh, S., & Guestrin, C. Anchors: High-Precision Model-Agnostic Explanations. www.aaai.org